宝くじは当たらない。

【はじめに】
　大みそかには、年末ジャンボ宝くじの抽選がありますが、正しくは「当たらない」ということではありません。ここでは、宝くじの当たる確率について考えてみます。

【1等の当選確率】
　正しくは、年末ジャンボ宝くじは、2千万分の１で1等が当たります。この2千万分の1という確率について、実感がありますか？
　日本の人口が約1億5000万人なので、全国民が１枚ずつ買っても、7～8人しか1等が当たらないのです。

【プロスペクト理論】
　プロスペクト理論とは、1979年に行動経済学者であるダニエル・カーネマンとエイモス・トベルスキーが提唱した理論で、「人が合理的に判断しているつもりでも、実際には『損失を大きく感じる』心理が働き、意思決定が歪むメカニズム」といわれています。また、同様に利益も大きく感じるとも言われています。

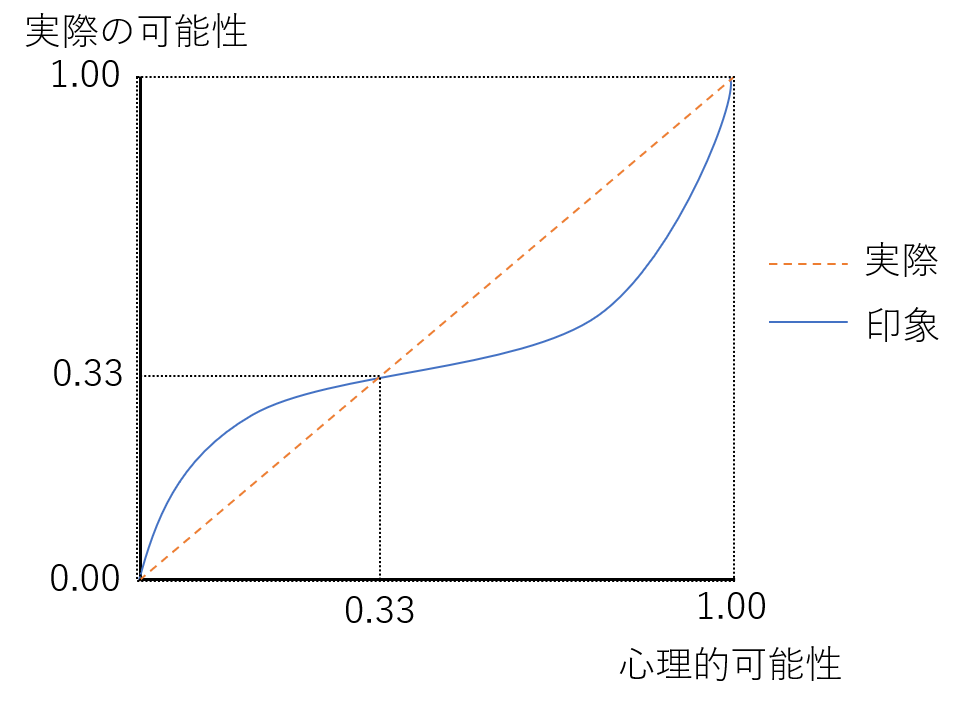
　具体的には、低い実現可能性には過大に評価し、高い実現可能性には過少に評価すると考えられ、その分岐点は、統計的に0.33（3分の1）程度と見込まれています。（左図）
　宝くじのように2千万分の1といわれても、母数が大きいために、例えば2万分の１との差が千倍もあると考えずに、「もしかしたら当たるかも」と考えてしまいます。
　逆に、特効的な新薬が開発されたが、「2千万人にひとりの確率で効果がない」といわれたら、自分がその一人かもしれないと過大に考えてしまいます。

【宝くじ必勝法（？）】
　私は、別の機会に同旨のコラムを書いたことがあるのですが、その時には多くのご意見を頂戴しました。
　内容は、「宝くじを1枚だけ買うわけではない」、「私は何十枚買っているので、当り確率は何十倍だ」など、宝くじマニアからのご意見が多かったと記憶しています。
　確かに2枚買えば、当たる確率も2倍ですが、外れる確率も2倍です。つまり利益に寄与するわけではありません。
　もっと言えば、連番で2千万枚購入すれば、確実に1等は当たります。しかしながら、確実に1999万枚の外れ（というか1等以外）の山が出来上がります。
　宝くじの還元率は50％弱なので、1枚300円の年末ジャンボ宝くじを60億円支出して、2千万枚購入すれば、確実に1等が当たりますが、当選金の合計は30億円弱になります。

【おわりに】
　ところで、プロスペクト理論に当てはめると、じゃんけんは心理的にも公平にできていると思うのですが、どうでしょうか。